Assignment ): Tutorial 4-2 Gum Drop Fish Assignment will be graded (2 points) from packet #13 will be graded. Download the GumdropBigFish world
Assignment 1 ) Miles Per Gallon: Create a world in which the
- Create 3 variables :
miles, gallons ,MPG
- 2 of the variables store the return value of a function
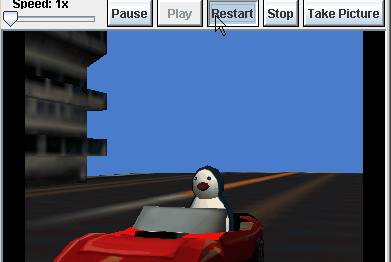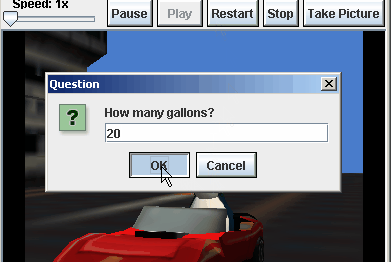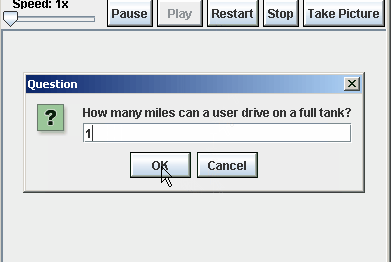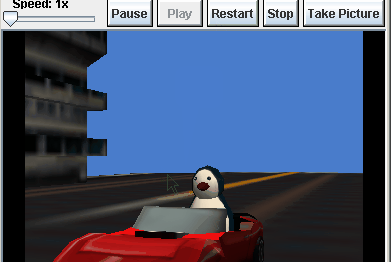
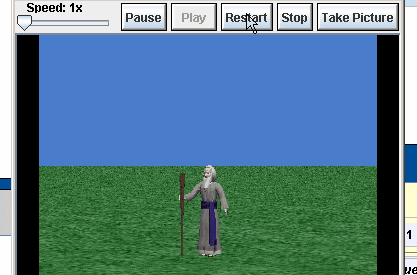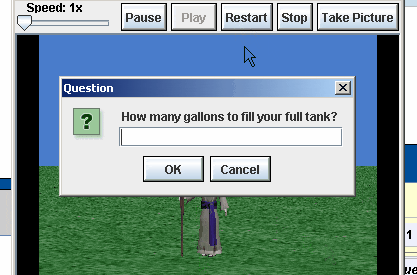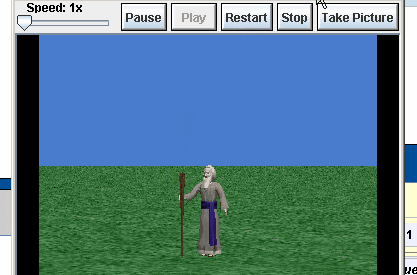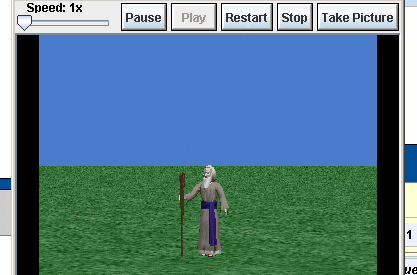
- The user is asked for the number of
gallons of fuel his or her car can hold. Use the return value of the ask use for a number function as shown below.
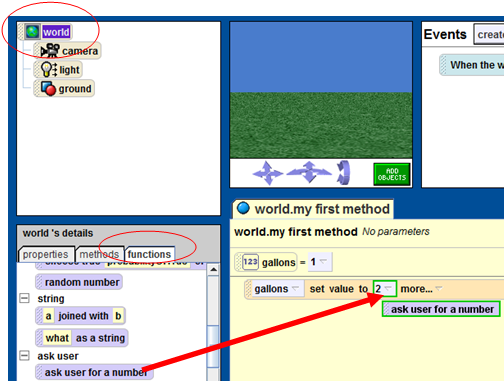
- Do the same thing for the the number of miles that he or she can drive on a full tank. Use ask a user function to set the value of the miles variable.
- The user is asked for the number of
gallons of fuel his or her car can hold. Use the return value of the ask use for a number function as shown below.
- 2 of the variables store the return value of a function
- a third variable called
MPG. This one will store the result of some math and will hold the car’s miles-per-gallon (MPG). Calculate the MPG with the following formula

1MPG = miles/gallons - At the end , your character should say the value of the mpg , as shown below.
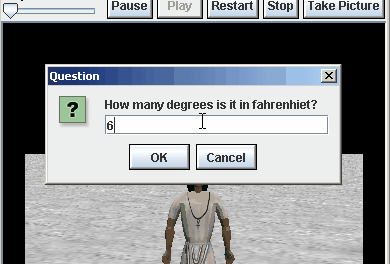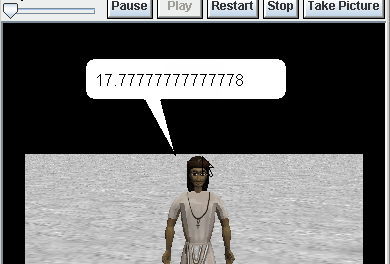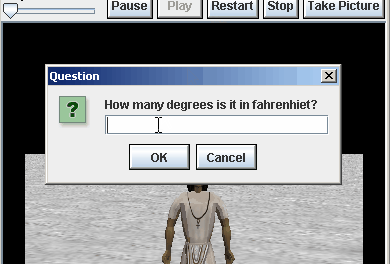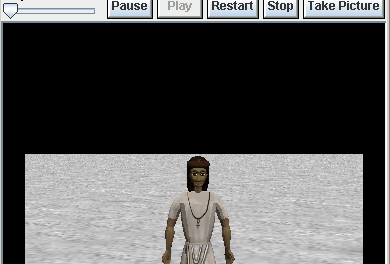
Assignment 3) Fahrenheit to Centigrade :
First, watch the animated gifs on this web page that explain how to use math in Alice
- Create a variable called degreesFahrenheit .
- Store the return value of the ask_user to enter a number function
- You should ask them for the degrees in Fahrenheit
- Create a variable called degreesCentigrade
- Use the following formula to convert the
degreesFahrenheit to Centigrade using the following formula
1degreesCentigrade = (5/9) * (degreesFahrenheit − 32) - use a character from the
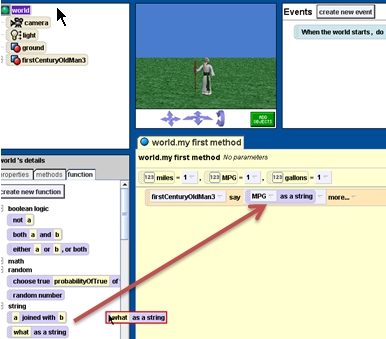
Peoplecollection to say the centigrade temperature. - Don’t forget that you can’t say numbers, you must use what as a string
Assignment 4) Modification of MPG
reopen the miles per gallon project
- if the MPG variable < 20
- say “What a Gas Guzzler”
- else
- say ” Your car is not a gas guzzler”
Assignment 5) Modification of Fahrenheit to Centigrade
reopen the Fahrenheit to Centigrade project and add
- if the degreesCentigrade variable <30
- say “It’s Very cold
- else
- say ” It is warm outside”
Assignment 6) Circle’s Area and Circumference: Create a world with your choice of person from the Peoplecollection. When you play the world, it should
- ask the user for the radius of a circle. (This value should be stored in a variable ).
- The person should then say the area and the circumference of the circle.( Links for the circumference formula , area of a circle)
- (For an extra point do the same thing with a “Sphere“. Ask the user for the radius and calculate the surface area and the volume.
Assignment 8
Roman Numeral translator
Here’s a gif showing partial code and what the finished project should look like
Objective : to let the user type in a number between 1 and 10 and then have a character “translate” that into Roman Numerals ( I, II, III, IV, V, VI, VII, VIII, IX, X)
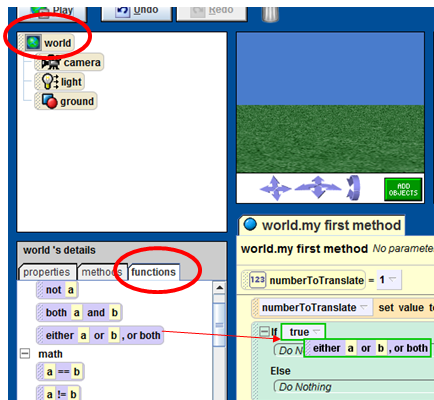
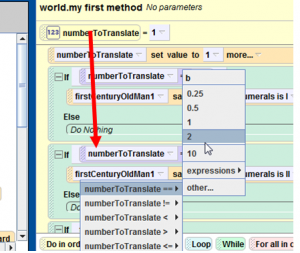
- Ask the user for a number and store the return value into a variable called numberToTranslate
- if the user enters a number greater than 10 then OR less than 1 , have your character say, use either a or b “Only enter numbers between 1 and 10”
- use a series of “if/else tests to translate the number and say the write translation for each number between 1 and 10
We are going to use the roman Numeral Translator file again, so it’s important that you don’t lose the file and give it a good name that you can easily recognize in the future.
Assignment 7-extra credit ). Look up the formulas for the volume and surface area of a cylinder . Ask the user for the height of the cylinder and the radius, which should be stored in variables. Then calculate the surface area and volume of the cylinder . See if there is a cylinder shape in the gallery to use as a visual aid.
Assignment 8 ) Open Assignment
Create an Alice world that
- uses a variable
- uses a ask_user world function
- uses a comment
- uses an if/else
- uses a math expression with more than one operation (ie addition and also multiplication or multiplication and also subtraction)
- tells a story













 http://
http://