Tag Archives: java

String Lab Assignment [loops]

In this lab, you will work with a GUI to validate the input in each text field . Below is a screenshot of the running program.

validate-user-input

 

  1. download the code: Validate Form Loop Version Starter Code 
  2.  If you’re using bluej, you want to run “main” as shown herevalidate-form-bluej
  3. Find the code section shown below. This is the one and only 1 area that you should be editingscreen-shot-code
  4. Validate the user input as described below:
  1. Name
    1. length of 3 >=
    2. only letters (spaces is ok)
  2.  Email
    1. Must include an “@”
    2. Must include a “.”
    3. the “.” must come after the “@”
  3. Phone
    1. XXX-XXX-XXXX
      1. where each”X” must be an integer value
      2. each “-” must be in the correct location
  4. Date of Birth
    1. To convert a String to an integer use Integer.valueOf(String str)
    2. Max age is 110
    3. Minimum accepted age is 18
      1. If the user is less than 18, display the message. “Sorry you must at least 18 years of age for this service”
  5. Password
    1. Length must be at least 5
    2. cannot include the name anywhere inside the password
  6. Zip Code
    1. Each character must be an integer
    2. Length between 3 and 5 , inclusive

 

If the user has no errors, then please show the message “Thanks for submitting your information ” , as shown below

validate-form_thx_for_submitting_V2

 

A  file that does a few test cases (be careful not to overwrite your work)

Class Relationships involving interfaces and Abstract Classes

Two Caveats

  1. all instance variables must be explicitly written as “private”
  2. Declare ArrayList’s as type “list”:
    1.  List<Integer> blahBlah = new ArrayList<Integer>()
    2. list-arraylist

 

The classes below represent different ways of representing mathematical  concepts like MathExpressions, Fractions etc. and they all implement the Mathable interface. 

 

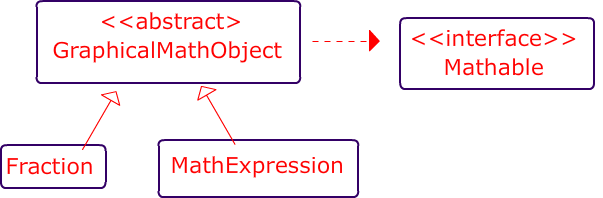
graphical_math_object

 

public abstract class GraphicalMathObject

methods

  • public abstract void displayGraphicalRepresentation() ;

public class Fraction extends GraphicalMathObject

This class is used to represent Fractions

Instance Variables

  • private int numerator
  • private int denominator

Constructor : The constructor should initialize both instance variables

  • public Fraction(int num, int denom)

Methods

  • public void displayGraphicalRepresentation() ; (just print out ” I’m a fraction -displayGraphicalRepresentation()”. This is the method that renders a graphical representation of the fraction .
  • fraction-matching
  • private int getGCF() //returns the GCF of numerator and denominator
  • public void simplify()//simplifies the fraction. Note: you must call getGCF()
  • public Fraction clone() //return a clone of the current object (** Extra credit…research this) ( link )
  • plus all of the methods in Mathable (Described at bottom)

public class MathExpression extends GraphicalMathObject

This is a class that is used to represent mathematical expressions like 3x2or 5x2y2 . It contains the methods and variables described below and it must implement Mathable

Instance Variables

  • private int coefficient
  • private List<String> variables
  • private List<Integer> powers

NOTE: you should use the following sytnax

Declare ArrayList’s as type “list”:

  1.  List<Integer> blahBlah = new ArrayList<Integer>()
  2. list-arraylist

Constructor : You can decide how to write the constructor.

  • Just be sure to initialize the instance variables

methods implement all methods of the Mathable Interface in ways that make sense for this class. The idea with Mathable is that you should be able to tell if the objects are either equivalent, exactly the same and that you should be able to return a String representation (data) that uniquely identifies the given mathematical expression.

  • public void addTerm( String term , int power) ) // This is used to represent multiplication, actually and this method adds a term with a power to the object’s list of variables and power to the list of powers. You can not assume that the term does not yet exist in the expression .
    For instance, if the original term were 3x5 and the object called addTerm("y", 6)  the object would then be 3x5y6. Or for another example, if the original term is 2x3z6 , and  addTerm("z", 5)  the object would be 2x3z11 .
  • public void displayGraphicalRepresentation()  ; (just print out “I”m a MathExpression.: displayGraphicalRepresentation()”). This is the method that draws the MathExpression on the screen like:
  • plus all of the methods in Mathable

Examples

3x2y5

coefficient: 3

variables : [ “x”, “y”]

powers : [ 2, 5]
x1y11

coefficient: 1

variables : [ “x”, “y”]

powers : [ 1, 11]
3y2x5

coefficient: 3

variables : [ “y”, “x”]

powers : [ 5 , 2]

 


Interface : Mathable

  • public String getData( ) ;   represents core mathematical information that defines current object.
  • public boolean exactlyEquals(Mathable other) ;
  • public boolean isEquivalent(Mathable other) ;

Super Classes Are Great I

 

Question: What limitations seem to exist with our use of classes?

 

I. Implement all Methods of the Triangle and Rectangle methods below

right_triangle_rectangle

 

Class: Rectangle  download-bttnRectangle

Constructor 

  • public Rectangle ( int  _col,  double  _width,  double _height)

instance Variables

  • private int color;
  • private double width;
  • private double height ;

Accessor Methods

  • public double getArea(); //returns the area of the rectangle
  • public int getColor()

 

Class: RightTriangle  download-bttnRightTriangle

Constructor 

  • public RightTriangle( int _col,  double  _width,  double _height)

instance Variables

  • private int color;
  • private double width;
  • private double height;

Accessor Methods

  • public double getArea(); //returns the area of the triangle
  • public int getColor()
  • public double getHypotenuse() ;

Class: InteractiveMath

download-bttn InteractiveMath-Arraylists (USE THIS ONE)

instance Variables

  • ArrayList<Rectangle> rectangles;
  • ArrayList<RightTriangle> triangles;

Accesor Methods

  • public double computeNetArea(){ //@ returns the area of the rectangles and triangles

 

Next  : Super Classes are great 2

Then  : constructors and inheritance.

after that : What is “Inherited” by Subclasses?

 

 

interactiveMath_arrays