One of the hardest concepts for younger programmers to learn is what returning a value means, a concept which Alice represents by its notion of ‘functions’. And, in Alice, a great approach is to require students to move an object based on the distance and to use a function to return the value of that distance and store it in a variable.
Every object in Alice has a set of proximity functions:

However, distance to, which most students will probably be most tempted to use is rarely what you want to use–especially when you want to move an object relative to another object using the calculated distance.
Consider, the picture below. Let’s say we want to calculate the distance between the hammer and the moon’s surface. Well, if you used distance to to calculate the distance and move the hammer down, you’ll see that the hammer actually falls down into the moon. That’ s because the distance is being calculated from the center of the hammer and the center of the whole planet!
Instead, use distance above!
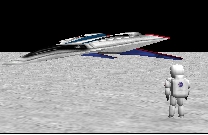
In the picture below, if you want the astronaut to move to the spaceship based off of a distance, you should try the distance in front of
Before you jump into text coding with middle school coders , Alice is a powerful tool for teaching what “returning a value” means.